Eigenvalores e eigenvectores

In algebra linear, un eigenvector de un function es un vector cuje direction non es cambiate per application de iste function. Iste vector ita debe esser differente del vector de nullo. Ergo un eigenvector solmente pote esser multiplicate per un scalar que on nomina le eigenvalor del function.

Le matrice de transformation ${\bigl [}{\begin{smallmatrix}2&1\\1&2\end{smallmatrix}}{\bigr ]}$ parallel a ${\bigl (}{\begin{smallmatrix}1\\1\end{smallmatrix}}{\bigr )}$ (in blau) e ${\bigl (}{\begin{smallmatrix}1\\-1\end{smallmatrix}}{\bigr )}$ (in violette). Le puntos in le linea trans le origine, parallel a un eigenvector, remane in linea post le transformation. Proque le vectores in rubie non son eigenvectores, lor direction es alterate per le transformation. Nota que le vectores blau son scalate per un factor de 3. Iste es lor eigenvalor associate. Le vectores violette non son scalate, ergo lor eigenvalor es 1.

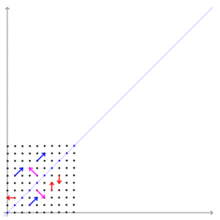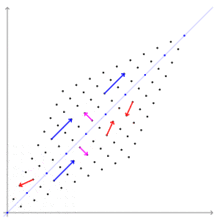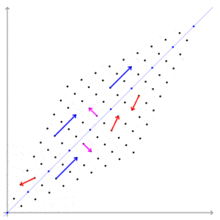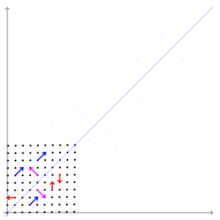
Si $T$ es un transformation linear de un spatio vectorial $V$ super un corpore $F$ in se e $\mathbf {v} \in V$ es un vector que non es le vector de nullo, tunc $\mathbf {v}$ es un eigenvector de $T$, si $T(\mathbf {v} )$ es un scalar multiple de $\mathbf {v}$. Iste condition pote esser scribite como le equation

$T(\mathbf {v} )=\lambda \mathbf {v} ,$

ubi $\lambda \in F$ es un scalar que es le eigenvalor associate con le eigenvector $\mathbf {v}$.

Le terminologia

In le diverse linguas, eigenvector tamben ha le nomine vector proprie o vector characteristic o autovector. Le prefixo eigen~ – cognoscite per cata experto – es un solution conveniente: eigenvector, eigenvalor, eigenspatia, eigendecomposition, eigenpolynomio, eigenfacie, eigenfunction etc.